
Toissa kerralla löysimme kolme tapaa mitata vektorin pituus. Kaikille kolmelle löytyi käyttötarkoitus, mutta arkielämässä vain yhdestä on hyötyä. Viime kerralla taas huomasimme, että arkinen mitta on kolmikon ainoa, jonka kanssa voi puhua kulmista. Mutta miksi asialla on merkitystä? Minkä vuoksi olen esittänyt pituusmittoja tasavertaisina, ja minkä takia ollut niin innoissani kulmien määrittelystä?
Syy on siinä, että kaikki, jonka parissa työskentelen matemaatikkona, on vektoria.
Jos tulet mukaan vasta tässä kohtaa, suosittelen aloittamaan yllä mainituista osista. Mutta varoituksen sana: en kertonut totuutta ensimmäisessä osassa.
...Tarkkaan ottaen, en sentään valehdellut. Tein vain niin kuin suurimmassa osassa lukio-opintoja, eli kerroin pikkaisen yksinkertaistetun version koko totuudesta. Määrittelin vektorin seuraavasti:
Vektori on suure, jolla on suunta. Se vastaa pistettä koordinaatistossa.

Sitten annoin kasan esimerkkejä vektorien ominaisuuksista. Tavallinen lukiomatikan tunti siis: ei olla ihan täsmällisiä, mutta yritetään tehdä kaikille selväksi, mistä on kyse. Ihan tervetullutta vaihtelua yliopistomatikkaan, jossa välillä ollaan niin ylpeän eksakteja, mutta kukaan ei tajua mistä varsinaisesti on kyse.
Nykyään minä määrittelen vektorin näin:
Vektori on vektoriavaruuden alkio.
Aika kiva kehäpäätelmä, eikö? Melkein kelpaisi vitsikirjaan, elleivät vitsikirjojen valmistajat harvemmin pitäisi matematiikkaa hauskana.
Pointti onkin siinä, että en määrittele vektoriavaruutta "vektoreista koostuvaksi avaruudeksi". Sen sijaan sanon:
Vektoriavaruus on joukko, jossa:
- Alkioita voi laskea yhteen niin, että tulos kuuluu joukkoon.
- Alkioita voi kertoa reaaliluvulla niin, että tulos kuuluu joukkoon.
- Yhteen- ja kertolaskuja voi yhdistää ja hajottaa tavallisin säännöin.
- On jokin alkio (nollavektori), jolla ei ole vaikutusta yhteenlaskussa.
Nämä ovat täsmälleen ne ominaisuudet, jotka tulivat esille esimerkeissä! Vitsin sijaan kyseessä onkin siisti temppu. Joku matemaatikko meni taannoin keksimään, että vektorit voikin määritellä tällä tavoin nurinpäin, ihan kuten joku oivalsi, että pituudelle voi antaa monta erilaista tulkintaa. Kuten pituudenkin kanssa, tämä avaa ihan uusia tulkintoja.
(Sivuhuomautus pedanteille: Reaalilukujen tilalle voitaisiin laittaa myös kompleksiluvut. Sillä vain ei ole tällä kertaa mitään väliä. En sanonut, että kertoisin nytkään ihan koko totuutta!)
Otetaan kaksi polynomia...
Vedetään hatusta kaksi täysin tavallista polynomia: \[ f(x) = 1 + 2x + 3x^2,\\ g(x) = 4 + 5x + 6x^2. \]- Voiko niitä laskea yhteen? Toki voi, $f(x) + g(x) = 5 + 7x + 9x^2$.
- Voiko niitä kertoa reaaliluvulla? Toki voi, $\alpha f(x) = \alpha + 2\alpha x + 3\alpha x^2$.
- Toimivatko osittelu- ja liitäntälait? Toki, tarkistakoon kuka jaksaa.
- Onko olemassa nolla-alkio? Toki on, $h(x) = 0$.
Toisin sanoen: myös polynomit ovat vektoreita.
Jos tämä olisi podcast, soittaisin tässä kohtaa dramaattista musiikkia, mutta onneksi tämä ei ole.

Tavallaan tulos ei yllätä yhtään. Voidaanhan $1 + 2x + 3x^2$ kirjoittaa myös muodossa $(1, 2, 3)$ ja sopia, että se tulkitaan oikealla tavalla. Siispä toisen asteen polynomit ovat jokseenkin sama asia kuin kolmiulotteiset pisteet. Yhtäsuuruus ei ole muuten ilmeinen, mutta vektorimuodossa kirjoitettuna asia ei voisi toisin ollakaan.
Toisaalta kaikki toisen asteen polynomit ovat kuin kolmannen asteen polynomeja: edellinen voidaan kirjoittaa myös $1 + 2x + 3x^2 + 0x^3$ tai $(1, 2, 3, 0)$. Sama pätee toki neljännen asteen polynomeille, eli yhtä lailla sen voisi kirjoittaa $(1, 2, 3, 0, 0)$. Voisiko olla järkevää puhua "minkä tahansa asteen" polynomeista ja sanoa $(1, 2, 3, 0, 0, \ldots)$?
Toki olisi. Taas dramaattista musiikkia.
Uusi määritelmämme vektorille ei mitenkään kiellä ääretönulotteisten vektoreiden olemassaoloa, joten sellaisten keksiminen on paitsi sallittua myös kannustettavaa. Näitä ei yleensä enää kutsuta polynomeiksi, mutta ei anneta sen haitata.
(Taas huomautus pedanteille: Ei ole mielekästä sanoa, että $(1,2,3) = (1,2,3,0)$. Kyse on kahdesta eri avaruudesta. Niiden välillä on kuitenkin erittäin luonnollinen yhteys, joka löytyy hakusanalla aliavaruus.)
Miten pitkä on polynomi?
Kun nyt olemme puhuneet monta jaksoa vektoreiden pituudesta, niin looginen askel olisi mitata polynomi. Mikä olisi järkevä tapa määritellä polynomin pituus?
Yksi tapa voisi olla käyttää polynomin kertoimia kuten pisteen koordinaatteja. Esimerkiksi polynomin $1 + 2x + 3x^2$ "pituus" olisi siis tavallisessa normissa $\sqrt{1^2 + 2^2 + 3^2} = \sqrt{14}$. Vielä kätevämmin taksinormissa se olisi $|1| + |2| + |3| = 6$, ja ihan ylivoimaisen helposti maksiminormissa $3$.
Ongelmia seuraa, kun tätä ideaa yrittää soveltaa yleisemmällä tasolla. Miten pitäisi määritellä "äärettömän polynomin" $1 + x + x^2 + x^3 + \ldots$ pituus? Maksiminormissa vastaus on totta kai $1$, mutta muissa normeissa tulos onkin $1 + 1 + 1 + \ldots = \infty$. Tämä ei ole kiva juttu, sillä pituuden soisi olevan äärellinen luku.
Yksi normin ominaisuuksista oli, että vektorin kertominen luvulla $\alpha$ kertoo vektorin pituuden luvulla $|\alpha|$. Äärettömän ottamista mukaan laskuihin tuli kokeiltua jonkun aikaa sitten, eikä jälki ollut kaunista.
Pitkää matikkaa pitkälle lukeneet saattoivat tunnistaa, että valitsemani "ääretön polynomi" on toiselta nimeltään geometrinen sarja. Se sattuu olemaan hyvin määritelty vain, kun $-1 < x < 1$, ja siinä tapauksessa \[ 1 + x + x^2 + \ldots = \frac{1}{1-x}. \]

Siinä missä tavalliset polynomit ovat järkeviä kaikilla luvuilla, tämä funktio toimii siis vain pienessä osassa lukusuoraa. Toinen ongelma: on olemassa muitakin funktioita kuin polynomeja. Miten esimerkiksi kuvan porrasfunktion pituus pitäisi määritellä? Tämä kaveri ei ole lähelläkään polynomia, joten kertoimista on turha puhua.

Äärellisen polynomin pituuden voi oikein hyvin määritellä edellä mainitulla tavalla, mutta yleisesti ottaen tarvitaan parempi keino. Sen pitäisi toimia muillakin kuin polynomeilla ja tarvittaessa vain osaan lukusuorasta rajoittuen.
Kelpaisiko integrointi? No kyllä! Sattuu olemaan niin, että funktion ja x-akselin välinen pinta-ala täyttää kaikki ehdot. Voimme siis vain laskea vaikkapa \[ \int_{-1}^{1} |1 + 2x + 3x^2| \,dx = 4. \]
Pieni miinus on, että polynomien tapauksessa täytyy rajoittua jollekin lukusuoran pätkälle; muuten nimittäin paukahdettaisiin taas äärettömyyksiin. Aika usein kuitenkin tämä riittää, ja vaihtoehtoisia tapoja on paljon. Itse asiassa polynomeista ei usein ole mitään väliä, ja niiden sijaan tutkitaan funktioita joiden integraalin voi laskea koko lukusuoran yli.
Samat kummalliset normit, joihin tutustuimme koordinaatistossa, toimivat tässäkin tapauksessa. Maksiminormin voi korvata funktion suurimmalla etäisyydellä x-akselista. Pythagoraan lauseen vastineen taas pystyy luomaan muokkaamalla integraalia pikkaisen: \[ \sqrt{\int_{-1}^{1} \left(1 + 2x + 3x^2\right)^2 \,dx} \approx 3.5. \]
Kohtisuorat funktiot
Mikä tekikään Pythagoraan normista niin yleispätevän? Se liittyi kulmien laskemiseen: Kahden vektorin kulma saatiin niiden välisestä pistetulosta. Vaikkapa vektorien $(1, 2)$ ja $(3, 2)$ välinen pistetulo on $1 \cdot 3 + 2 \cdot 2 = 7$, ja tämä jakamalla vektorien pituuksilla saadaan niiden välisen kulman kosini.

Tavallisessa normissa oli se erikoisuus, että sen saattoi ilmaista vektorin pistetulolla itsensä kanssa: $|v| = \sqrt{\langle v, v \rangle}$. (Tällä kertaa merkitsen pistetuloa kulmasulkeilla, jottei se sekaannu kertolaskuun.)
Tuossa edellisessä integraalissahan funktio kerrotaan itsensä kanssa.
Kahden funktion väliseen pistetuloon on siis kaava \[ \langle f, g \rangle = \int_a^b f(x) g(x) \,dx, \] ja funktioiden pituus on hyvin tunnettu. Tästä seuraa, että osaamme laskea kahden funktion välisen kulman!
Tämä kulma ei liity mitenkään funktioiden graafiseen esitykseen – sitä ei voi piirtää kuvaajalle. Tässä on kaksi polynomia ($1+x^2$ ja $(1+x)/2$), jotka eivät edes kosketa toisiaan. Silti ne ovat kohtisuorassa toisiinsa nähden välillä ${[{-1},{1}]}$!

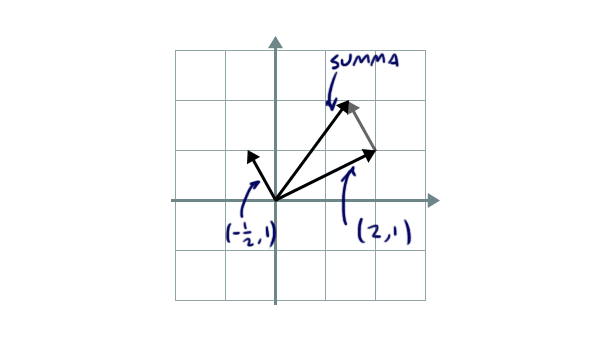
Tämä touhu alkaa kuulostaa enenevässä määrin abstraktilta humpuukilta, mutta kaikkeen on syynsä. Viime kerralla puhuimme siitä, kuinka vektorin voi esittää toisten vektoreiden summana:
Jos funktiot ovat vektoreita, niin silloin funktioita voi esittää toisten funktioiden summina. Edellä nähtiin jo, kuinka ääretön polynomi olikin sama kuin tietty osamäärä. Toinen klassinen esimerkki on sinifunktio, joka on sama kuin ääretön polynomi \[ \sin x = x - \frac{x^3}{6} + \frac{x^5}{120} - \frac{x^7}{5040} + \ldots. \]
Funktioiden esittäminen äärettöminä summina on laaja tutkimusala, josta kirjoitin aiemmin otsikolla Teekkarin ja teoreetikon ylin ystävä. Se on äärimmäisen käytännöllinen ala: vaikkapa joka kerta, kun räpsäiset selfien itsestäsi lukemassa matikkablogeja, kameran ohjelmisto muuntaa kuvapisteet funktioksi, siirtää sen summamuotoon, terävöittää sieltä ja silottaa täältä, ja lopuksi tallentaa tuloksen pieneksi pakattuun tiedostomuotoon.
1900-luvun alkupuolella syntynyt funktionaalianalyysi on matematiikan lohko, joka tutkii funktioita ääretönulotteisina vektoreina. Siinä tutut operaatiot saavat uudet muodot: esimerkiksi derivointi tarkoittaakin pisteen kuvaamista toiseksi pisteeksi. Ongelmat muuttuvat paljon helpommiksi, kunhan vain keksii sopivan avaruuden ja kätevän pistetulon (joita on enemmänkin).
Tästä ajattelutavasta on hyötyä, koska kaikki vektoreille pätevät ominaisuudet pätevät saman tien funktioille. Lukiossa opitaan esimerkiksi laskemaan pisteen etäisyys suorasta. Suora voidaan kirjoittaa summaamalla vektori ja toisen vektorin monikerta. Lähin suoralla (kuten myös tasolla) sijaitseva piste muodostaa suoran kulman:

Ihan samalla tavoin voidaan summata funktioiden monikertoja "suorien" muodostamiseksi. Sama suoran kulman sääntö pätee yhä, joten meillä on saman tien tapa löytää jotakin hankalaa funktiota parhaiten arvioiva funktio helpompien funktioiden joukosta.
Viime kerralla mainitsin myös lineaariset kuvaukset, jotka säilyttävät vektorin esityksen kantavektoreiden summana: \[ f(a\bar v + b\bar w) = a f(\bar v) + b f(\bar w). \]
Nyt annan esimerkin lineaarisesta funktiosta. Sitä voidaan merkitä kirjaimella $D$, ja sen nimi on derivaatta. Tässä on nyt vähän Inception-meininkiä, mutta derivaatta on funktio, joka ottaa funktion ja antaa tulokseksi funktion. Lisäksi jokainen muistaa summan ja vakiokertoimen derivointisäännöt: \[ D(af(x) + bg(x)) = a f'(x) + b g'(x). \]
Lineaarisiin funktioihin liittyy paljon mukavaa teoriaa esimerkiksi ratkaisujen lukumäärään liittyen. Siksi derivaattaa on helppo käsitellä esimerkiksi differentiaaliyhtälöissä, joissa yritetään ratkaista tuntematon funktio. (Esimerkiksi $f''(x) = -f(x)$. Kokeile jotain trigonometrista ratkaisuksi! Kuinka monta ratkaisua keksit?)
Funktionaalianalyysi on yliopiston maisteritason matikkaa, mutta sen perusteet eivät ole kovinkaan kaukana lukiosta. Ääretönulotteisuus tekee teoriasta syvän ja välillä yllättävän, ja tuloksilla on arvoa hyvin monella alalla. Differentiaaliyhtälöitä käytetään kaikissa luonnon- ja insinööritieteissä, mutta lisäksi vaikkapa kvanttifysiikka puhuu funktionaalianalyysin kieltä.
Ihanaa kun joku jaksaa kirjottaa näistä! Lisää!
VastaaPoistaMahtavaa jos näistä on iloa!
Poista