Vektori ja sen pituus

Kuvassa on kolme ympyrää. Kuinka niin?

Kun minä olin nuori, vektorit jakoivat mielipiteitä. Tarkoitan siis, että lukiossa osa piti niistä ja osa ei päässyt jyvälle niiden logiikasta. Fysiikkaa lukeneet muistavat piirrelleensä mallikuviin nuolia ja siten päätelleensä mihin suuntaan laatikko/curlingkivi/veturi/jäätä pitkin liukuvan limupullon nappaava alieni (eikö teidän lukiossa?) liikkuu.

Yliopistomatikassa vektoreita käytetään ehkä yllättävän paljon ja tavoilla, joita ei heti ajattelisi. Meillä painopiste ei ole laatikon liikkeissä vaan ihan muissa jutuissa, joissa ei välttämättä näy pisaraakaan geometriaa. Tässä ja parissa seuraavassa tekstissä

• käymme läpi, mitä vektorit oikein ovat,
• kohtaamme kummallisia juttuja, kuten väitetyt kolme ympyrää, ja
• selvitämme, miksi matemaatikko haluaa nähdä vektoreita kaikessa, mikä ei liiku.

Suunta ja suuruus

Aloitetaan ihan peruskysymyksestä: mikä ihme on vektori? Olen kirjoittanut asiasta aiemminkin pelien koodailun muodossa, kauan sitten ekan vuoden yliopistolaisena. Kolmen vuoden varrella olen kasvanut, kyynistynyt ja vieraantunut todellisesta maailmasta, mutta yksi asia pysyy: pieni kertaus on aina paikallaan.

Vektori on suure, jolla on suunta. Se vastaa pistettä koordinaatistossa. Esimerkiksi $(2, 1)$ on kaksiulotteinen vektori, joka piirretään nuolena origosta pisteeseen, joka on kaksi yksikköä x-akselin suuntaisesti ja yhden yksikön y-akselin suuntaisesti:

Fysiikassa vektoreita käytetään kuvaamaan esimerkiksi nopeutta tai voimaa: ylipäänsä mitä tahansa, jolla on paitsi suuruus myös suunta. Tällöin vektorit voivat hyvin olla kolmeulotteisiakin. Ulottuvuuksien määrällä ei ole periaatteessa mitään rajaa.

Samanlaisia vektoreita voi laskea yhteen. Tämä ilmaistaan laskemalla komponentit yhteen ja kuvallisesti piirtämällä nuolet peräkkäin: \[(2, 1) + (-\tfrac 1 2, 1) = (\tfrac 1 2, 3)\]

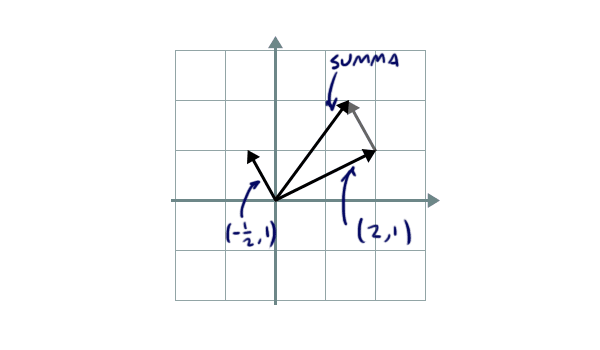
Esimerkiksi jos laatikon kahteen vierekkäiseen sivuun asentaa rakettimoottorit, niin boksi liikkuu vektoreiden summan mukaisesti vinosti. (Ennen kuin ilmanvastus tekee liikeradasta kaoottisen ja luultavasti räjähdykseen päättyvän. Älä kokeile tätä kotona, ja linkkaa video kun kokeilet kuitenkin.)

Lisäksi vektoria voi kertoa jollain luvulla, ja tulos on sama kuin komponenttien kertominen: $3 \cdot (1, 2) = (3, 6)$. Kertolasku muokkaa siis vektorin pituutta. Nollaa pienemmällä luvulla kertominen kääntää vektorin suunnan vastakkaiseksi, mutta muuten suunta ei muutu kertolaskussa.

Yksikköympyrä ja sen kaverit

Vektorin pituudesta puheen ollen, kuinka pitkä on vektori? Kuvasta löytyy suorakulmainen kolmio, joten pituus löytyy Pythagoraan lauseen avulla: (Sivumennen sanoen, Pythagoraan lause on varmaan väärinnimetyin asia matematiikan historiassa. Pythagoras on yli tuhat vuotta "lausettaan" nuorempi!)

Kaksiulotteisessa tapauksessa tulokset on helppo tarkistaa ruutupaperilla ja viivaimella, mikäli joku sellaisia vielä nykyaikana käyttää. Sama periaate toimii myös kolmessa ulottuvuudessa, joten esimerkiksi vektorin $(1, 2, 3)$ pituus on $\sqrt{1^2 + 2^2 + 3^2} = \sqrt{14}$.

Vaihdetaan aihetta ihan hetkeksi. Puhutaan ihan pikkaisen siitä, mikä on ympyrä. (Uskoisitko, että minulla on yliopistotutkinto matematiikasta? En aina minäkään.)

Matemaattisesti määriteltynä ympyrä on se joukko pisteitä, joka on kiinteällä etäisyydellä keskipisteestä. Ehdottomasti tärkein esimerkki on yksikköympyrä, eli ne pisteet jotka ovat yhden yksikön etäisyydellä origosta:

Okei, palataan nyt vektoreihin. Pituuden laskeminen Pythagoraan lauseella on ihan kivaa, mutta eikö olisi yhtään helpompaa tapaa? Kaikkien noiden neliöjuurien kanssa pitää kaivaa laskin esiin. Entä jos on allerginen juureksille tai vakaumuksellinen lihansyöjä?

Kun vektorin nyt voi kirjoittaa muodossa $(1, 2)$, niin eikö vain voitaisi sopia $1+2=3$? Paljon helpompi laskea!

Yksi pieni mutka kyllä tulee matkaan; nimittäin jos vektori onkin $(1, -2)$, niin pituus menee miinusmerkkiseksi. Mutta ollaan pahiksia, unohdetaan vain ne miinukset, otetaan itseisarvo!

Niin, ja on toinenkin pieni mutka. Jos vektorin $(x, y)$ pituus on $|x| + |y|$, niin yksikköympyrä näyttää tältä:

...Se ei ole ympyrä. Paitsi että itse asiassa se on.

Niin oudolta kuin se kuulostaakin, kyseessä ei ole pieleenmennyt yritelmä vaan ihan oikea ympyrä. Vektorin pituuden voi määritellä ihan hyvin myös tällä tavoin, jos ummistaa silmänsä siltä pikkujutulta, että viivoitin saattaa antaa eri lukuja. Matemaattisesta näkökulmasta pituuden riittää toteuttaa kolme ehtoa:

• $(0, 0)$ on ainoa vektori, jonka pituus on nolla.
• Jos vektoria kertoo luvulla $\alpha$, niin myös vektorin pituus kerrotaan luvulla $\alpha$ (etumerkkiä lukuunottamatta).
• Kolmion minkä tahansa kahden sivun yhteispituus on suurempi kuin kolmannen sivun pituus.

Mitä hyötyä sitten on näin laveasta määritelmästä? No, tätä vaihtoehtoista pituutta kutsutaan myös taksi- tai Manhattan-normiksi. Nimi tulee New Yorkin ruutukaavasta, jossa kadut menevät tiukasti pääilmansuuntien mukaan. Jos haluaa kulkea kaksi korttelia koilliseen, täytyy kulkea kaksi ruutua itään ja kaksi pohjoiseen. Matkaa on siis neljä korttelinmittaa.

Hauska juttu on, että määritelmä sallii vieläkin yksinkertaisemman pituusmitan: otetaan vektorin isoin komponentti (taas miinukset unohtaen). Toisin sanoen $(1, 2)$:n pituus onkin tämän "maksiminormin" mukaan kaksi yksikköä.

Jos jostain tieteelle tuntemattomasta syystä haluat lähettää postipaketin, niin maksu määräytyy yleensä paketin pisimmän sivun mukaan. Tämä pituusmitta on siis se, jota postilaitokset käyttävät. Sen tuottama yksikköympyrä näyttää tältä:

Siinä on ympyrän neliöintiä parhaimmillaan! Toisin sanoen jos paketin yksi sivu on metrin mittainen, niin postimaksu ei muutu oli toinen sivu sitten kymmensenttinen tai puolimetrinen.

Silti... mikä saa matemaatikon pitämään kaikkia kolmea tapaa yhdenvertaisina tapoina mitata pituus? Ovatko yliopistolaiset taksien ja pakettien suurkuluttajia, pitääkö verovarojen käytöstä olla kenties huolissaan?

Yksi syy on tietenkin se, että jos yhdellä ja samalla teorialla saa selitettyä arkiset mitat, taksimatkat ja postinjakelun, niin se on parempi kuin kolme erillistä teoriaa. Toisekseen, joissakin tilanteissa ei ole mitään väliä, mitä näistä kolmesta käyttää. Syy on siinä, että kaikki kolme menevät sisäkkäin:

Nämä pituusmitat ovat vakiokertoimen sisällä toisistaan. Yhdellä tavoin mitattu pituus on vähintään puolet ja enintään tuplasti toisen pituusmitan verran. Tämä riittää takaamaan, että mitoilla on samat ominaisuudet. Ja sehän on kätevää – Pythagoraan lauseen neliöjuurta on pikkaisen hankala muokkailla, joten miksipä ei todistettaisi väitteitä helpommilla kaavoilla!

Esimerkiksi työprojektissani käytän laskukaavaa, johon syötetään pisteiden välisiä etäisyyksiä. Tämä kaava ei välitä siitä, mitä pituutta käytetään (kunhan yhtä vakiotermiä säätää), joten totta kai lasken etäisyydet helpoimmalla tavalla. Se on tietokoneenkin näkökulmasta näppärämpää.

Jotain eroa näiden pituusmittojen välillä kuitenkin täytyy olla. Mitä Pythagoraan kaavalla on takataskussaan, jotta se toimii arkielämässä? Mikseivät taksi- ja postipakettinormit ole luonnollisia? Se selviää ensi kerralla.

---

Bonus: Ei tässä ollut läheskään kaikkia tapoja määrittää pituutta! Saatat muistaa (ja jos et muista, niin se ei haittaa), että $\sqrt x$ on sama asia kuin $x^{1/2}$. Sama pätee muillekin juurille. Siispä Pythagoraan lause on itse asiassa sama kuin \[ \left(|x|^2 + |y|^2 \right)^{1/2}. \]

Merkitsin itseisarvomerkit, jotta yhtäläisyys taksinormin kanssa olisi selkeämpi: \[ \left(|x|^1 + |y|^1 \right)^{1/1}. \]

Näissä kahdessa on siis jotain samaa. Herää kysymys, voisiko kakkosen korvata jollain muulla luvulla. Vastaus on kyllä vain; millä tahansa luvulla $p \geq 1$ voidaan määritellä pituus \[ \left(|x|^p + |y|^p \right)^{1/p}. \]

Mitä suuremmaksi $p$ kasvaa, sitä enemmän yksikköympyrä muistuttaa maksiminormia. (Tässä on hyvä GeoGebra-harjoitus lukiolaiselle.) Tästä syystä jälkimmäistä kutsutaan myös $\infty$-normiksi.

Jos $0 < p < 1$, niin yksikköympyrän kaaret painuvat sisäänpäin ja tulos muistuttaa tuikkivaa tähteä. Tällöin kuitenkaan kolmion sivujen pituutta koskeva ehto ei enää toteudu.