Kahden vektorin kulma

Viime kerralla havaitsimme, että pituuden voi laskea monella tapaa. Pisteestä pisteeseen voi kulkea linnuntietä tai taksilla, ja New Yorkin ruutukaavassa tulokset ovat erittäin erilaiset. Kahdesta erilaisesta pituusmitasta seuraa myös kaksi erilaista ympyrää, ja niistä vain toinen on pyöreä.

Kuitenkin arkielämässä on vain yksi tapa laskea pituus. Remonttihommissa ei hirveästi auta selitellä Manhattan-normia, kun huoneen kulmasta kulmaan pitäisi mitata palkki: ainoa tapa on sivu toiseen plus sivu toiseen ja neliöjuuri.

Jos kaikki pituuden määritelmät olivat muka yhtä päteviä, niin mikä sitten tekee Pythagoraan kaavasta niin ylivoimaisen?

Pistetulos tai ulos

Niin kuin matematiikassa yleensä, puhutaan hetki jostain ihan muusta ja päädytään alkuperäiseen kysymykseen muutaman kiertotien sekä keittiön ikkunan kautta.

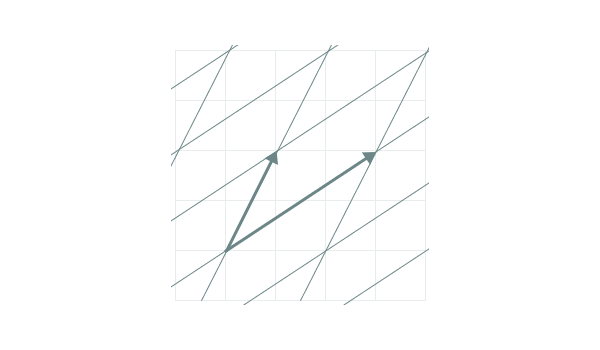
Otetaan kaksi vektoria, sanotaan vaikka $(1,2)$ ja $(3,2)$. Ne näyttävät kuvassa tältä:

Mikä on näiden vektoreiden välinen kulma, jota kuvassa merkkaan kreikan kirjaimella $\theta$ eli theeta? (Miksi juuri theeta? Se nyt vain näyttää kivalta, ja sitä käytetään aika usein kulmien merkkaamiseen. On se ainakin helpompi piirtää kuin $\xi$.)

Kyllähän ihan jokainen osaa tuon kulman laskea. Täydennetään vain kuva kolmioksi, lasketaan sivujen pituuksia, selataan inspiraatiota MAOL-taulukoista, piirretään varmuuden vuoksi muutama kolmio lisää, kokeillaan kosinilausetta ja lopuksi mietitään, miksi oikein valitsi pitkän matematiikan.

Tai ainakin siltä se minusta tuntuu. Minulla taitaa olla joku trauma geometriasta.

Ei se kosinilause oikeasti niin vaikea ole.

Onneksi on olemassa helpompikin tapa. Se menee muutamassa vaiheessa. Ensiksi lasketaan vektorien pistetulo, joka saadaan kertomalla komponentit keskenään ja summaamalla tulokset: \[ (1,2) \cdot (3,2) = 1 \cdot 3 + 2 \cdot 2 = 7. \]

(On vähän epäonnista, että samaa pistettä käytetään myös tavallisena kertomerkkinä.)

Sitten jaetaan saatu luku vektorien pituuksilla. Tässä kohtaa pitää käyttää sitä perinteistä Pythagoraan lausetta: $\sqrt{1^2 + 2^2} = \sqrt{5}$ ja $\sqrt{3^2 + 2^2} = \sqrt{13}$. Nyt on lupa vetää laskin esiin ja naputtaa jakolasku sisään. Tulokseksi saadaan \[ \frac{7}{\sqrt{5} \cdot \sqrt{13}} \approx 0{,}87. \]

Entä sitten? No, paina vielä sitä nappia jossa lukee $\cos^{-1}$ tai ehkä $\arccos$. Näytölle ilmestyy \[ 0{,}87 \approx \cos 30^\circ. \]

Jos haluat tarkistaa, menikö oikein, voit joko luottaa minuun tai sommitella kulmaviivainta lukulaitteesi näytölle. Suosittelen tietenkin jälkimmäistä.

En tiedä, oliko tämä loppujen lopuksi juurikaan vaivattomampaa, mutta minusta tämä on helpompi tapa muistaa. (Kosinilause on sama kaava toisessa muodossa, joten ei ole väliä kumpaa käyttää.) Täsmälleen sama kaava pätee myös kolmessa – tai vaikka kymmenessäkin – ulottuvuudessa.

Pythagoraan erityisasema

Kaiken lisäksi tämä tapa selittää, mitä matemaattisesti erikoista on siinä tavallisessa pituusmitassa. Edellä nähty kaava kahden vektorin $\bar v$ ja $\bar w$ kulmalle löytyy MAOL-taulukoista: \[ \cos (\bar v, \bar w) = \frac{\bar v \cdot \bar w}{|\bar v| |\bar w|}, \] missä $|\bar v|$ on vektorin $\bar v$ tavallinen pituus. Voit kokeilla, että tämä kaava ei toimi muilla viime kerralla esitetyillä pituusmitoilla, jotka vektorille $(2,1)$ olivat siis $|2|+|1|$ ja $\max\,(2,1)$. Miksei?

Entä jos $\bar v$ ja $\bar w$ ovat sama vektori? Tällöin kulma on nolla astetta ja nollan kosini on yksi: \[ 1 = \frac{\bar v \cdot \bar v}{|\bar v| |\bar v|}. \]

Kerrotaan pituudet pois nimittäjästä ja otetaan neliöjuuri: \[ |\bar v| = \sqrt{\bar v \cdot \bar v}. \]

Mutta tämähän on vain vähän mutkikkaampi tapa sanoa, että jos $\bar v = (x, y)$, niin sen pituus on \[ |\bar v| = \sqrt{x^2 + y^2}. \]

Toisin sanoen kyse ei olekaan siitä, että kulman kaavassa pitää käyttää tavallista pituusmittaa, jotta tulos olisi järkevä. Pikemminkin Pythagoraan pituusmitta on seurausta pistetulosta.

Tietenkin historiallisesti Pythagoras tuli ensin ja pistetulo seurasi perässä muutaman vuosituhatta myöhemmin. Matematiikan kannalta on kuitenkin kätevämpää määritellä ensin pistetulo ja johtaa siitä pituusmitta kaavalla $\sqrt{\bar v \cdot \bar v}$. Syy on nimittäin siinä, että toisenlaisissa vektoriavaruuksissa voi olla vaikeaa keksiä kätevää pituusmittaa, mutta helppoa keksiä pistetulo.

Samalla selvisi, miksi Pythagoraan lause on ainoa oikea. Koska se nivoutuu pistetuloon ja sitä kautta kulmakaavaan, se on ainoa pituusmitta, jonka kohdalla on "luonnollista" puhua kulmista.

(Tarkkaan ottaen pistetuloja on äärettömän monta, koska komponenteille voi antaa painokertoimia. Kertoimet venyttävät koordinaatistoa akseleiden suuntaisesti.)

Monta tapaa sanoa sama piste

Yksi näppärä, joskin lukiossa ehkä vielä vähän selittämätön, sovellus vektorien kulmille löytyy kantavektoreista. Idea on, että mikä tahansa kaksiulotteinen vektori voidaan esittää yhdistelmänä kahdesta vektorista, jotka eivät ole samansuuntaisia. (Ja sama korvaamalla "kaksi" jollakin muulla luvulla.)

Esimerkiksi yllämainitut vektorit $(1,2)$ ja $(3,2)$ muodostavat kannan, koska ne ovat erisuuntaisia. Jokainen vektori $(x,y)$ on muotoa \[ (x,y) = a(1,2) + b(3,2) = (a + 3b, 2a+2b) \] joillekin luvuille $a$ ja $b$. Nämä luvut ovat vieläpä uniikit.

Visuaalisesti tulos näyttää koordinaatistolta, jota on venytetty:

Mitä hyötyä tällaisesta esityksestä on?

Yksi etu on siinä, että se helpottaa laskuja. Aika usein vektoreita käsitellään niin sanotuilla lineaarisilla kuvauksilla. Sellaisille pätee \[ f(a\bar v + b\bar w) = a f(\bar v) + b f(\bar w). \]

Tämä näyttää vähän hankalalta mutta ei ole oikeasti paha. Jokainen vektori voidaan esittää kahden kantavektorin yhdistelmänä. Funktion tulos taas voidaan esittää kahden tulosvektorin yhdistelmänä. Tulosvektorit saadaan kantavektoreista ja kertoimet pysyvät samoina.

Toisin sanoen funktio $f$ voi olla ihan hirvittävän vaikea laskea. Jos kuitenkin tiedämme sen arvot kahdessa pisteessä (jotka eivät ole samalla suoralla), osaamme saman tien sanoa sen arvon ihan missä tahansa päin xy-tasoa!

Tietenkään useimmat funktiot eivät ole lineaarisia. Yllättävän moni kuitenkin on.

Toinen etu saadaan, jos kantavektorit ovat vieläpä kohtisuorassa toisiinsa nähden. Kohtisuoruus on loistava juttu. Sitä kautta voidaan johtaa kaava pisteen etäisyydelle suorasta (MAOL on ystävä tässäkin). Lähin suoralta löytyvä piste muodostaa nimittäin suoran kulman:

Hienot nimet asioille

Otetaan vielä lopuksi pikkaisen historiaa. Vektorien nykyinen tulkinta on syntynyt 1900-luvun taitteessa. (Jos yksityiskohdat kiinnostavat, vilkaise Historia Mathematica -lehden artikkelia. Lehti on tieteellinen ammattilehti, mutta teksti on vapaasti luettavissa.)

Vektoriavaruutta, jossa on määritelty jokin pituusmitta sekä yksi tekninen lisäehto (joka lukiossa toteutuu), kutsutaan myös Banachin avaruudeksi. Stefan Banach (1892–1945) oli puolalainen matemaatikko, joka muutaman maanmiehensä kanssa kehitti topologiaa (jatkuvien muunnosten tutkimusta) sekä funktionaalianalyysia. Viimeksi mainittu tarjoaa paljon lisää esimerkkejä Banachin avaruuksista. Mitä taas 30-luvun puolalaiseen matikkaan tulee, se onkin oma kiinnostava tarinansa jollekin toiselle kerralle.

Avaruutta, jonka pituusmitta perustuu pistetuloon, sanotaan joskus Hilbertin avaruudeksi. David Hilbert (1862–1943) onkin tutumpi nimi matematiikan harrastajalle. Hänet muistetaan esimerkiksi Hilbertin hotellista, keinosta havainnollistaa erilaisia äärettömiä joukkoja. Hän myöskin loi kunnianhimoisen – ja tuhoon tuomitun – ohjelman matematiikan perusteiden selvittämiseksi. Hilbertin avaruus on siitä harvinainen käsite, että sen nimi todella viittaa yhteen sen kehittäjistä.

Mutta mitä on tämä funktionaalianalyysi, jota kumpikin herra oli luomassa/löytämässä? Miksi intoilin lineaarisista kuvauksista ja pisteen etäisyydestä suorasta? Se selviää sarjan päätösosassa!