Ai miksikö nollalla ei saa jakaa? No ensinnäkin siksi, että niin ei saa tehdä. Toisekseen siksi, että kuvahaku sanalle "division by zero" tuottaa tämän tuloksen:
![Google-kuvahaku on maailman toiseksi siteeratuin akateeminen lähde. [Google-kuvahaku 2018] Google-kuvahaku: division by zero](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgH16prA3dGS1DBxEQ9v-hfFoHQpw2flsDtIvzQoj51D_BwuVmp8WREYkRta0R7FZTi-SMFTSj2WnWkYwXzoJC-v2Je7fVxWZKYo76_t5ERRK66JfjpigF7pI4CETKJnqdMn7L3GmMfqJ8M/s1600/Kuvahaku.jpg)
Mikäli asia tuli tästä selväksi ja olisi parempaakin tekemistä, voit lopettaa lukemisen nyt. Helppoa! Mutta jos "siksi" ei kelpaa vastaukseksi, katsotaanpa asiaa hieman tarkemmin...
Miksei $1/0 = \infty$?
Yleisin ratkaisu nollalla jakamiseen on todeta tuloksen olevan ääretön. Hallituissa olosuhteissa — tai fysiikassa — se voi olla ihan pätevä vastaus. Onhan ilmiselvää, että luvut kasvavat kohisten nollaa lähestyttäessä: \[1/1 = 1,\] \[1/0.01 = 100,\] \[1/0.000001 = 1~000~000\] ja niin edelleen.
Tämän perustelun esittäjä tosin unohtaa sellaisen pikkupikkujutun, että negatiiviset luvut ovat olemassa. Ihan samalla logiikalla nimittäin \[1/(-1) = -1,\] \[1/(-0.01) = -100,\] \[1/(-0.000001) = -1~000~000\] eikä todellakaan voida puhua mistään plus äärettömästä. Siis pitäisikin sanoa, että yksi jaettuna nollalla on $\pm \infty$. On se nyt aika kehnoa, että yksinkertaisesta jakolaskusta tulee kaksi vaihtoehtoista lukua.

...ja olisikin se vain näin vähän väärin. Ääretön nimittäin ei edes ole luku. Ei ole luvun tapaista, että $\infty + 1 = \infty$. Kaatunut kahdeksikko tarkoittaa jotain paljon hienovaraisempaa kuin yksittäistä konkreettista lukuarvoa.
No miksei vaikkapa $1/0 = 0$?
Niin, jospa oikea vastaus olisi sitten äärettömien puolessavälin? Se ei toimi, koska silloin nolla voidaan kertoa nimittäjästä pois:
\[ \frac 1 0 = 0 \Leftrightarrow 1 = 0 \cdot 0. \]Matematiikassa on joitakin perusperiaatteita, joista on hyvä pitää kiinni. Yksi niistä on se, että $1=0$ ei ole merkki onnistuneesta päättelystä.
![[Puolue josta et pidä] vaalikampanjan keskeinen ajatus. Jos 1=0, niin minä olen tasavallan presidentti.](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhmSMv5n8JUI62uxtr7ByogVVTCoxFEKzfUmEIZb4IRU8iAEWPj1KPd6OCABcmjOoNQ9J3s52QisIhHa2ijNpHo_XHGhpTq3tPxBt_YQI7BHMBimGE3kho7yQPZomXrfC4BRyO2bEoxeTS0/s1600/Presidentti.png)
Miksei $0/0=1$?
Tämä itse asiassa on hyvä kysymys! Funktion $x/x$ kuvaaja kun näyttää jokseenkin tältä:
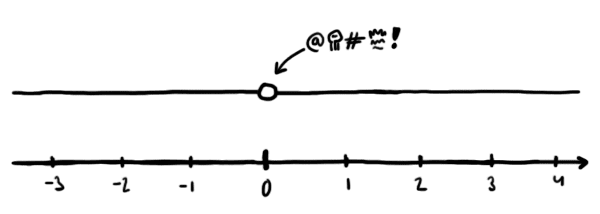
Aika ilmiselvästi (varsinkin raja-arvoihin tutustuneelle) nolla per nollan pitäisi olla yksi. Samanlainen toteamus voidaan tehdä luvulle $0^0$ — kyllähän sen pitäisi olla yksi. Joissakin tilanteissa voi olla melkein sopivaa sopia, että näin onkin. Kuitenkin edellinen virhe toteutuu tässäkin:
\[ \frac 0 0 = 1 \Leftrightarrow 0 = 0 \cdot 1 = 0. \]Hetkinen, eihän tuo ole virhe: kyllä nolla on yhtä kuin nolla. Niinpä niin, mutta myös tämä on totta:
\[ \frac 0 0 = 17 \Leftrightarrow 0 = 0 \cdot 17 = 0. \]Nolla per nolla on näemmä mikä tahansa luku. Se taas on pienimuotoinen probleema, mikäli jakolaskun halutaan olevan hyvin määriteltyä. Tämän saman voi ilmaista myös toisella tavalla. Varmaankin halutaan, että $0 \cdot 1 = 0$. Mutta toisaalta
\[ 0 \cdot 1 = 0 \cdot \frac 0 0 = \frac{0 \cdot 0}{0} = \frac 0 0 = 1. \]Fine, tästä ei tule mitään. Nollalla jaettaessa ei voi saada mitään reaalilukua, ikinä.
No olisiko $\def\oo{\ddot o} 1/0=\oo$?
Samanlaisia argumentteja vain on kuultu aiemminkin. Kaikkihan tietävät, että $\sqrt{-1}$ on täysin luvaton juttu kirjoittaa. Aika moni tietää myös, että on olemassa imaginaariluku $i$, joka on juurikin tuon laskun tulos. (Tarkkaan ottaen ratkaisuja on kaksi, $\pm i$.)
Kompleksiluvuissa on se jännä puoli, että ne ovat täydellinen laajennus reaaliluvuille. Kaikki laskusäännöt toimivat edelleen, vaikka kummalliset kuvitteelliset luvut kuokkisivatkin kekkereissä. Olisiko mahdollista tehdä sama luvulle $1/0$?
Sovitaan, että $1/0 = \oo$. Mielestäni $\oo$ on harvinaisen hyvä kirjain tälle luvulle, paitsi siksi että se kuvaa käyttäjän suusta purkautuvaa ilmaisua, myös koska eräs matematiikan professori kannattaa vahvasti aliarvostettujen ääkkösten käyttöä matematiikassa. Katsotaanpa, säilyttääkö tämä ömityinen öliö laskusäännöt.
Matematiikassa käytetään usein aksioomiin perustuvaa etenemistapaa. Aksiooma on juttu, joka on niin ilmiselvä, että sen on pakko olla tosi. Reaalilukujen kaikki ominaisuudet saadaan johdettua neljästätoista aksioomasta. (Knoppitieto: kolmellatoista ensimmäisellä saadaan rationaaliluvut.) Laskusäännöt tulevat yhdeksästä ensimmäisestä, joten muut jätetään tänään sivuun.

Aloitetaan siitä aksioomasta, josta koko juttu lähti. Analyysin oppikirjani sanoo seuraavaa:
Jokaista reaalilukua $x \in \mathbb{R}$, $x \neq 0$, vastaa reaaliluku $y \in \mathbb{R}$ siten, että $xy=1$. Tällöin merkitään $y = \frac 1 x$ tai $y = x^{-1}$ (käänteisluku).
Aika yksinkertaista: käänteisluvut ovat tarpeellisia ja ne tuntuvat järkeviltä, joten eiköhän sovita niiden olevan olemassa. Nolla on poikkeustapaus, mutta meidän lisäyksellämme asia helpottuu:
Jokaista öklöä reaalilukua $x \in \mathbb{R}_ö$, vastaa öklö reaaliluku $y \in \mathbb{R}_ö$ siten, että $xy=1$. Tällöin merkitään $y = \frac 1 x$ tai $y = x^{-1}$ (käänteisluku).
Määritelmänsä mukaan $\oo$ eli $1/0$ on nollan käänteisluku. Koska luvun ja sen käänteisluvun tulo on yksikkö, tällöin on $0 \cdot \oo = 1$. Tämä on vähintäänkin kiinnostavaa; nolla kertaa $\oo$ ei siis olekaan nolla. Mikään aksiooma ei kuitenkaan kiellä tätä suoraan, joten uskallamme jatkaa. Otetaanpa tarkasteluun vielä toinen aksiooma.
Jokaista reaalilukua $x \in \mathbb{R}$ vastaa reaaliluku $y \in \mathbb{R}$ siten, että $x+y=0$. Tällöin merkitään $y = -x$ (vastaluku).
Tämän perusteella siis $\oo + (-\oo) = 0$. Yhteinen tekijä ottamalla siitä saadaan $(1-1)\oo$ eli tuttavallisemmin $0\oo$. Mutta äskenhän todettiin, että $0\oo = 1$ — hupsistakeikkaa, taas tuli todistettua $0=1$! Aksioomat eivät saa johtaa ristiriitoihin, koska silloin ne eivät todista yhtään mitään. (Ks. Matematiikan epätäydellisyys.)
Jos $\oo$ on nollan käänteisluku, niin ööllä ei ole vastalukua. Jos vastaluku löytyy, $\oo$ ei voi olla $1/0$. Kumpi pudotetaan pelistä? Vaihtoehtoina on palata lähtötilanteeseen, jossa $1/0$ ei ole määritelty, tai hylätä yhtälönratkaisemisen kulmakivi: ilman vastalukuja kun ei voi siirrellä termejä puolelta toiselle. Omasta mielestäni on aika selvää, kumpi vaihtoehto kannattaa.
On muitakin tapoja lisätä nollalla jakaminen matemaattiseen työkalupakkiin. Kaikki kuitenkin johtavat samaan tulokseen: jostain hyödyllisemmästä ominaisuudesta pitää luopua. Arkisiin tarpeisiin sellaisesta matematiikasta ei olisi iloa.
Ja siksi nollalla ei saa jakaa.
Psst... veikö algoritmi aikajanasi matematiikan puutostilaan? Tykkää Nollakohdan upouudesta Facebook-sivusta ja ole somen coolein ja kulturellein!
Oon aina aavistellut että matematiikka on oikeesti paljon enemmän, kiehtovampaa ja merkityksellisempää kun miltä se tuntuu koulussa, kiitos siitä että osoitit mun epäilykset todeksi mielenkiintosella ja ymmärrettävällä tavalla! Harmi että silti paljon mielummin luen sun blogitekstejä kuin lasken :)
VastaaPoistaMatt Parkerin vertausta lainatakseni koulumatikka on matikalle sitä mitä käsittelyharjoitukset jalkapallolle - havaintosi on ihan oikea! Laskemista on hyvä harjoitella, mutta se oikea hauskuus kyllä on ihan muualla, kuten blogit, Numberphile-videot ja (Suomessa vähän harvinaiset) kirjat osoittavat. Vasta yliopistolla päästään oikeaan asiaan käsiksi, mutta se onkin sitten vakavampaa...
PoistaKiitos kommentista, mukava kuulla näiden raapustusten onnistuvan tehtävässään! :D