Nollan ja ykkösen valtava väli

Kaikki tietävät, että lukuja on äärettömästi. (No okei, eivät kaikki, mutta tällä oletuksella menen.) Tämä äärettömyys ei ole vain leveää vaan myös syvää: pelkästään nollan ja ykkösen välissä on aika monta lukua.

Otetaan vaikka nollan ja ykkösen keskiarvo $\frac 1 2$. Ja tämän ja nollan keskiarvo $\frac 1 4$. Ja siitä saadaan $\frac 1 8$. Ja niin edelleen, loputtoman pitkään, aina nollaa lähestyen muttei sitä ikinä tavoittaen. Siispä pelkästään nollan ja ykkösen välissä on äärettömän monta rationaalilukua!

Sana "ääretön" kuitenkin vihjaa ongelmallisesti, että kyse olisi yhdestä, intuitiivisesta asiasta. Todellisuudessa ääretön ei ole kumpaakaan, mokoma rontti.

On kai aika ilmiselvää, että jos vain joka toinen kokonaisluku on parillinen, niin parillisia lukuja täytyy olla vähemmän kuin kokonaislukuja yhteensä? No eipä vaan ole. Jokaisen kokonaisluvun voi kertoa kahdella, jolloin saa parillisen luvun. Siispä niitä täytyy olla saman verran!

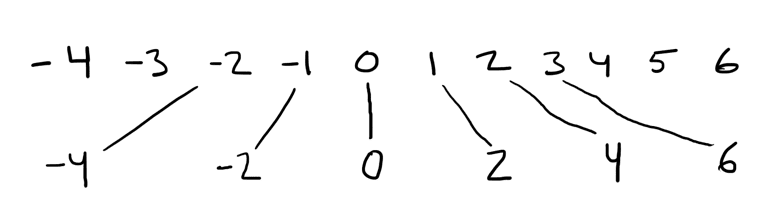
Paljon vaikeammin käsitettävä juttu on, että myös rationaalilukuja on saman verran kuin kokonaislukuja: onhan pelkästään nollan ja ykkösen välissä äärettömän monta rationaalilukua muttei yhtään kokonaislukua. Luvulle $a/b$ voi sopia vastinpariksi vaikka luvun $2^a 3^b$, joka on alkutekijähajotelman mukaan yksikäsitteinen. (Harjoitus lukijalle: täydennä tämä toimimaan negatiivisille rationaaliluvuille.) Jos jokaista rationaalia vastaa kokonaisluku, rationaaleja ei voi olla enemmän kuin kokonaislukuja!

Samanlainen juttu ei kuitenkaan onnistu reaalien kanssa. Reaalilukuja todella on enemmän kuin rationaali- tai kokonaislukuja. Tämän voi osoittaa helpolla kikalla: Pistetään kaikki reaaliluvut nollan ja ykkösen väliltä jonoon.

Sitten tehdään uusi reaaliluku: valitaan ensimmäiseksi numeroksi jokin muu kuin ensimmäisen luvun eka numero, toiseksi jokin muu kuin toisen toka numero ja niin edelleen. (Makuasia, miten numeron valitsee.) Nyt saadaan luku, joka eroaa jokaisesta listan luvusta ainakin yhdellä desimaalilla. Mutta sittenhän kyseinen luku ei ole listalla!

Jos oletus johtaa ristiriitaan, se voidaan kuitata virheelliseksi. Nyt päädyttiin siihen, että kaikkia reaalilukuja ei voi listata ikinä. Kokonaisluvut voi pistää järjestykseen ilman että mitään putoaa välistä — niinhän ne yleensä ajatellaan — joten reaaleja täytyy olla enemmän.

Ja jotta asiat olisivat vielä ihanampia, mehän tarkastelimme vain väliä $[0, 1]$. Mutta ei se mitään, koko lukusuoralla on yhtä monta reaalilukua kuin tuolla surkealla pikku välillä! (Esimerkiksi funktio $f(x) = \tan(\pi x - \frac \pi 2)$ tuottaa halutun yksi yhteen -vastaavuuden.)

No mitä nämä ylimääräiset ei-rationaaliset luvut sitten ovat? Kaikkein klassisin esimerkki löytyy kurkottamalla pikkuisen kauemmaksi nollasta, jonnekin puolentoista tietämille: $\sqrt 2$. Todistus sille, että $\sqrt 2$ ei ole rationaaliluku, on klassikkokamaa, joten toiston uhallakin käyn sen tässä läpi. Tämän uskotaan olevan jo Pythagoraan ajoilta, ja erityisesti legenda kertoo Pythagoraan palkinneen nerokkaan Hippasoksen menolipulla Välimereen löydöstään. (Pythagoras tykkäsi kokonaisluvuista.)

Oletetaan, että $\sqrt 2$ onkin jokin loppuun asti sievennetty rationaaliluku $a/b$. Koska antiikin kreikkalaiset eivät tienneet negatiivisista luvuista mitään, yhtälön voi surutta korottaa toiseen potenssiin:

\[ 2 = \frac{a^2}{b^2}. \]

Tämä tarkoittaa, että $2b^2 = a^2$ eli $a^2$ on parillinen. Se taas meinaa sitä, että $a$ on parillinen — voit tarkistaa itse, että näin on — ja silloin voidaan kirjoittaa $a=2k$. Laitetaan tämä uusi tieto edelliseen yhtälöön:

\[ \begin{align*} 2 &= \frac{(2k)^2}{b^2}\\ 2b^2 &= 4k^2\\ b^2 &= 2k^2. \end{align*} \]

Nyt ylläolevalla päättelyllä päästään siihen, että myös $b$ on parillinen. Mutta oletuksessahan luki "loppuun asti sievennetty"! Taas kerran tuli ristiriita, ja siksi $\sqrt 2$ ei ole rationaaliluku.

Jos tämä tuntuu seksuaaliselta toiminnalta välimerkin kanssa, olet jokseenkin oikeassa. Mutta matematiikassa näillä pienillä jutuilla on väliä.

Reaalilukujen ja rationaalilukujen eron voi tiivistää siihen, onko lukusuoralla aukkoja. Kyllä, jokaisen rationaaliluvun välistä löytyy äärettömän monta rationaalilukua. Mutta kuitenkin siellä täällä on kakkosen neliöjuuren näköisiä lukuja, jotka ovat reikiä rationaalisessa todellisuudessa. (Tässä "siellä täällä" tarkoittaa "oikeastaan kaikkialla".)

Vihjasin vähän aikaa sitten, että reaaliluvut ja rationaaliluvut perustuvat täsmälleen samoihin aksioomiin yhtä lukuun ottamatta. Se ilmenee nimenomaan tässä. Erilaisilla rationaaliluvuilla päästään mielettömän lähelle kakkosen neliöjuurta, mutta ei täsmälleen siihen. Viimeinen aksiooma, jota myös täydellisyysaksioomaksi kutsutaan, sanoo, että $\sqrt 2$ ja kumppanit ovat olemassa.

Tässä kohtaa asia menee jo aika tekniseksi, joten eiköhän ole parasta lopettaa. Voin luvata, että yliopiston raja-arvojen kurssilla asia... jää edelleen epäselväksi! Äärettömyys on vaikeaa!