
Tämänhetkinen tutkimusprojektini käsittelee fysiikan yhtälöitä, jotka kuvaavat aaltoliikettä. Yhtälöt itsessään etenevät kuin kellokoneisto ilman mitään satunnaisuutta, mutta minäpä tutkinkin, mitä tapahtuu jos lähtötilanne on satunnaisesti valittu. Viritän siis kuvitteelliselle vedenpinnalle satunnaisesti valitun muodon, käynnistän kellon ja katson, miten aallot alkavat loiskua.
(Oikeasti en tosin katsele mitään... työskentelen täysin teoreettisesti kynällä ja paperilla. En ohjelmoi simulaatioita eikä minua päästettäisi lähellekään aaltotankkia.)
Mutta miltä ylipäätään näyttää satunnaisesti valittu lähtötilanne? Millainen on satunnainen funktio? Tapoja sellaisen rakentamiseen on monta, joten eiköhän kurkata niistä muutamaan.
Tapa 1: jokainen piste on satunnainen
Aloitetaan helpoimmasta ideasta. Jos $x$ on lukusuoran piste, niin $f(x)$ on jokin siihen pisteeseen liittyvä lukuarvo. Entä jos valitaan jokainen $f(x)$ jollain satunnaisella tavalla, sanotaan nyt vaikka normaalijakaumasta? (Tarkkaan sanottuna standardista normaalijakaumasta, eli siitä jonka keskiarvo on $0$ ja keskihajonta $1$.)
Normaalijakaumassa nollan ympärillä olevat luvut ovat todennäköisimpiä, mutta periaatteessa siitä voi tulla ulos vaikka kuinka suuria tai pieniä lukuja. Kuitenkin suuren luvun todennäköisyys on häviävän pieni. Kuvaajalta näkyy, että suhteellinen todennäköisyys pienenee todella rajusti etäisyyden nollasta kasvaessa:

Väännetään siis rautalangasta, miten satunnainen funktio muodostetaan: $f(0)$ on normaalijakautunut luku, $f(1)$ on jokin toinen normaalijakautunut luku, ja niin ovat myös $f(0{,}5)$ tai $f(17\pi/3)$. Helppoa kuin heinänteko.
Kuvaajaksi piirrettynä tämä funktio näyttää tältä:

Heinänteko ei taidakaan olla helppoa? Mikä oikein meni pieleen?
Katsotaan vaikka pistettä $f(0{,}5)$, se on siinä kuvan keskellä vaikkei siltä näyttäisikään. Tässä pisteessä normaalijakauma antoi tällä kertaa arvoksi suunnilleen $0{,}7523$. Viereisessä pisteessä taas... niin, mikä onkaan viereinen piste? Lukusuoralla on pisteitä äärettömän tiheässä, joten jokaisen pisteen naapurustossa riittää tungosta.
Normaalijakaumasta tulee edes nelosta isompi luku todennäköisyydellä, joka on luokkaa 0.003 %. Satasta isomman luvun todennäköisyyttä ei edes saa helposti ulos tietokoneesta, se on niin naurettavan lähellä nollaa.
Ikävä kyllä häviävän pieni todennäköisyys kertaa äärettömän monta pistettä on edelleen äärettömän iso määrä pisteitä. Samaan aikaan hirvittävän suuressa määrässä pisteitä funktio on nollan läheisyydessä. Kaiken kaikkiaan satunnainen funktiomme siis sohii ja säheltää ympäriinsä pahemmin kuin kofeiinilla kyllästetty orava.
Näin huonosti käyttäytyvälle funktiolle ei voi tehdä paljon mitään matematiikan keinoin. Sitä on turha piirtää ja todella toivotonta derivoida. Koetetaanpa keksiä siis jokin fiksumpi tapa. Ihan turha yritys tämä ei kuitenkaan ollut, useammastakin syystä:
- Joskus on ihan tervettä nähdä, että matematiikassa kaikki ei suju kuin Strömsössä.
- On erittäin tervettä nähdä, että matemaattiset ongelmakohdat voivat olla muutakin kuin laskuvirheitä.
- Tämä menetelmä tekee näyttävän comebackin muutaman ruudunmitan kuluttua.
Tapa 2: kaikki rakastavat trigonometriaa
Jokainen teekkari ja teoreetikko tietää, että Fourier-sarjat ovat kova juttu. Perustelut löytyvät esimerkiksi luovasti nimetystä tekstistäni Teekkarin ja teoreetikon ylin ystävä, mutta tiivistetään ne vielä uudestaan tässä.
Sini- ja kosinifunktio tekevät täyden kierroksen välillä ${[{0},{2\pi}]}$. Tässä $2\pi$ on kulmamittaus radiaaneina ja tarkoittaa samaa kuin 360 astetta. (Matemaatikot suosivat radiaaneja syystä, joka mainitaan linkatussa tekstissä.) Kuvana ne ovat nämä tutut kaverit:

Funktiot $\sin(2x)$ ja $\cos(2x)$ tekevät vastaavasti kaksi kierrosta tällä välillä, $\sin(3x)$ ja $\cos(3x)$ kolme kierrosta ja niin edelleen.
Osoittautuu, että kaikki riittävän kivat funktiot välillä ${[{0},{2\pi}]}$ voidaan esittää äärettömän pitkänä summana tällaisista funktioista. Kaavan muodossa siis \[ f(x) = c + \sum_{n=1}^\infty \bigg( a_n \sin(nx) + b_n \cos(nx) \bigg), \]
missä $c$ on funktion keskiarvo ja kaikki kertoimet $a_n$ ja $b_n$ saadaan niin sanotulla Fourier-muunnoksella. Esimerkiksi funktio \[ f(x) = \sum_{n=1}^\infty \bigg( \frac{1}{n^2} \sin(nx) + \frac{(-1)^n}{n^2} \cos(nx) \bigg) \]
näyttää tältä erikoiselta sykkyrältä:
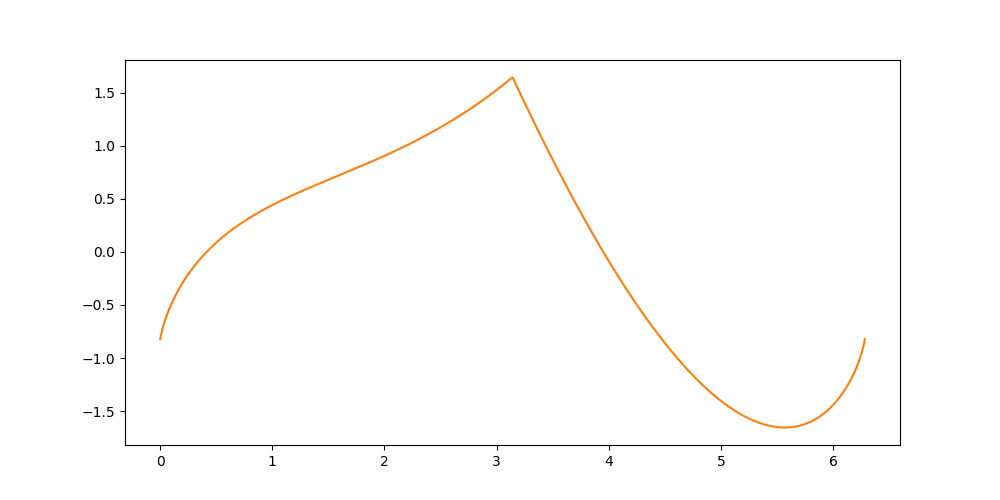
Olen laiska, joten sovitaan että keskiarvo $c=0$. Tällä tavoin jäljelle jää enää äärettömän monta termiä. Toistetaan nyt yllä tehty trikki ja nyhjäistään jokaiseksi kertoimeksi satunnainen luku!
Jos jokainen $a_n$ ja $b_n$ on normaalijakautunut luku, toisistaan riippumatta, niin ajaudumme samanlaiseen ongelmaan kuin edellä – äärettömän pitkään summaan mahtuu äärettömän paljon hankalia lukuja eikä summauksesta tule mitään. (Lukiossa tai myöhemmin raja-arvoja lukeneet tietävät, että summa hajaantuu.)
Mutta meillä on nyt käytössämme pikkaisen enemmän rakennetta kuin viimeksi. Voimme nimittäin käyttää indeksiä $n$ eduksemme. Jaetaankin $n$'s kerroin luvulla $n$. Kertoimet $a_1$ ja $b_1$ tulevat siis tavallisesta normaalijakaumasta, kertoimet $a_2$ ja $b_2$ puolet kapeammasta sellaisesta ja niin edelleen. Tässä siis normaalijakauman keskihajonta on $1/n$.
Ja nyt kaikki toimii! Ääretönkin summa on mahdollista laskea, kun termit pienenevät tarpeeksi nopeasti. Yksi esimerkki tällaisesta funktiosta on \[ f(x) = 0{,}1257 \sin(x) - 0{,}6635 \cos(x) - 0{,}0661 \sin(2x) - 0{,}3067 \cos(2x) + \cdots \]

Arvotaan kertoimet uudelleen ja saadaan erilainen funktio:

Jos minulta kysytään, niin tämä funktio ainakin näyttää satunnaiselta. Lisäksi se näyttää hyvin piikikkäältä. On mahdollista osoittaa, että tällä tavalla luodut funktiot ovat jatkuvia mutta eivät yhdessäkään pisteessä derivoituvia.
Tapa 3: pala kerrallaan
On olemassa toinenkin fiksu keino.
Ensimmäisessä yritelmässä ainoa varsinainen ongelma oli, että funktio sai pahasti erilaisia arvoja vierekkäisissä pisteissä. On kuitenkin näppärä tapa rakentaa funktio niin, että tätä ongelmaa ei ole.
Valitaan ensin välin päätepisteille satunnaiset arvot normaalijakaumasta, ja piirretään näiden väliin jana:
Sitten jaetaan jana puoliksi ja siirretään keskipistettä ylös- tai alaspäin. Siirtymä nyhjäistään normaalijakaumasta, jonka keskihajonta on $\sqrt{1/2}$:

Jatketaan samaa prosessia puolittamalla kumpikin puolikas ja lisäämällä $\sqrt{1/4}$-normaalijakaumat keskipisteisiin, ja niin edelleen. Jos tätä jatketaan äärettömän pitkään, niin lopputulos näyttää esimerkiksi tältä:

Itse asiassa tulos näyttää hyvin samanlaiselta kuin edellisessä menetelmässä, ja asia on matemaattisesti näin!
Tällaisella satunnaisella funktiolla on nimikin:

Yllä puolestaan on piirretty yksiulotteinen liike: aika kulkee vasemmalta oikealle, ja y-akseli kuvaa hiukkasen siirtymää lähtöpisteestä.
Dramaattinen paljastus
Brownin liikkeen tärkeä ominaisuus on, että pisteiden $x_1$ ja $x_2$ välinen erotus on normaalijakautunut keskihajonnalla $|x_1 - x_2|$. Edellä mainitsin, että liikkeellä ei oikeasti ole derivaattaa, mutta kokeillaan silti laskea se. Määritelmän mukaan derivaatta saadaan erotusosamääränä \[ f'(x) = \frac{f(x + h) - f(x)}{h}. \]
Osoittaja on satunnainen, ja sen keskihajonta on siis $|(x+h)-x|$ eli $|h|$. Nimittäjässä on $h$. Nämä kumoavat toisensa, ja jäljelle jää tavallinen normaalijakauma keskihajonnalla $1$. Siispä $f'(x)$ on normaalijakautunut luku.
Dun-dun-duu!
Ykköskohdassa kehitelty mahdoton sotku on siis Brownin liikkeen derivaatta, ainakin jos heilutellaan käsiä pikkaisen. Derivaattafunktiota kutsutaan valkoiseksi kohinaksi, ja se todella on ikävä funktio – mutta ainakin sitä on mahdollista integroida ja saada Brownin liike ulos.
(Nimi "valkoinen kohina" tulee siitä, että virittämättömästä radiosta kuuluva kohina näyttää kuvaajalle piirrettynä aika samalta. Valkoinen viittaa siihen, että äänen jokainen taajuus on samalla lailla satunnainen, ihan niin kuin valkoisessa valossa jokainen aallonpituus on yhtä voimakas. On olemassa eri "värisiä" kohinoita sen mukaan, miten taajuudet käyttäytyvät.)
Yleisesti ottaen kakkoskohdan rakennelmaa voi vähän muokata: $1/n$ ei ole ainoa mahdollinen valinta kertoimien keskihajonnaksi. Jos kertoimet pienenevät nopeammin (vaikka $1/n^{1{,}5}$ tai $1/n^2$), niin funktiosta tulee sileämpi ja derivoituvampi. Tämä johtuu siitä, että pahin siksakki tulee korkeammista "taajuuksista", joiden painokertoimet pienenevät nopeammin.

Tapa 4: ihan erilainen keino
Haluan nopeasti esitellä vielä yhden menetelmän kehittää satunnaisia funktioita. Entä jos valitaankin "melkein" vakiofunktio: funktio on muuten tasainen, mutta satunnaisin väliajoin se hyppää satunnaisen määrän?
Sovelluksia ajatellen on luonnollisinta valita hyppyjen suuruus normaalijakaumasta ja välimatkat niin sanotusta eksponenttijakaumasta. Eksponenttijakauma tuottaa aina nollaa suurempia lukuja siten, että pienet luvut ovat todennäköisempiä kuin isot.
Tällä keinolla syntyvä funktio näyttää jotakuinkin tältä:
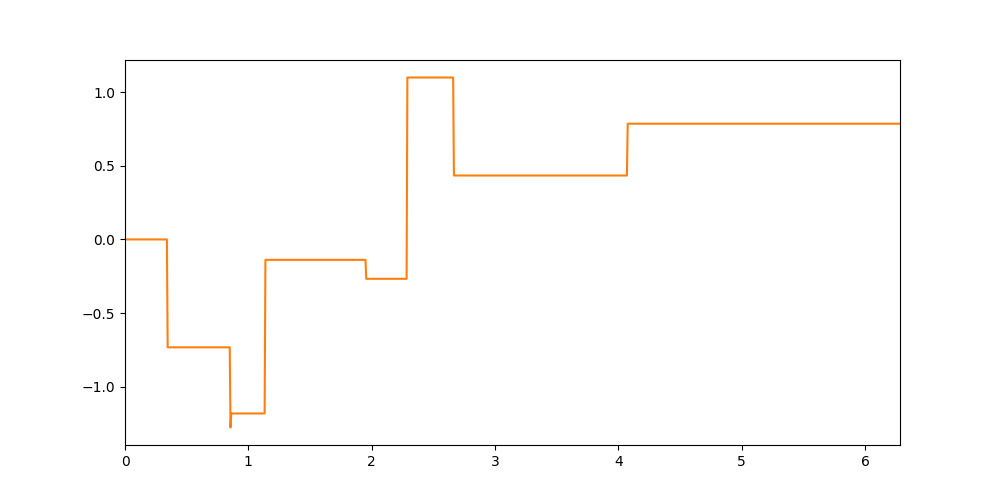
Kyllä tuotakin voisi hyvällä syyllä kutsua satunnaiseksi.
Vielä yksi idea! Entä jos plussataan tämänlainen funktio ja Brownin liike? Sittenhän saataisiin funktio, jossa on kahdenlaista satunnaisuutta: sekä satunnaista siksakkia että yllättäviä hyppäyksiä ja pudotuksia. Pikaisen yhteenlaskun tulos on:
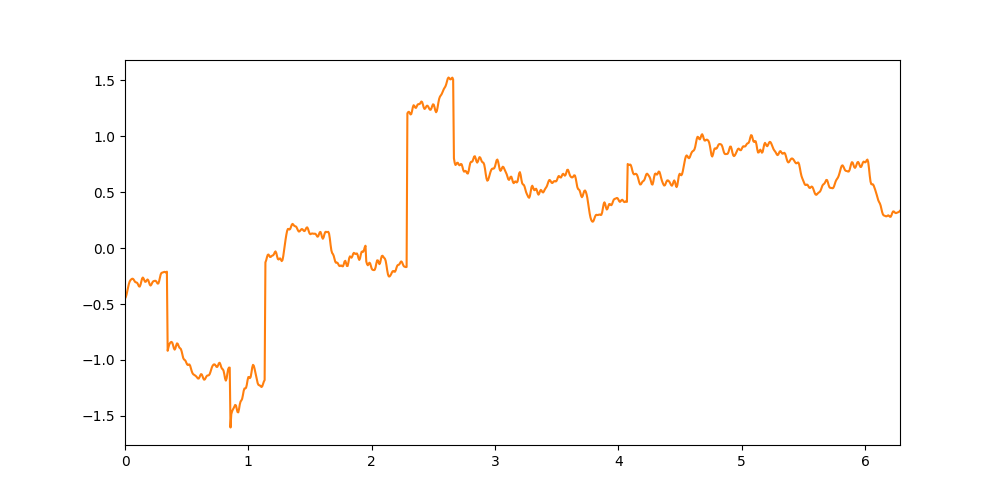
Tällainen jatkuvan ja hyppivän yhdistelmä on todella hyvä malli moneen käytännön ilmiöön, sanotaan vaikka pörssikursseihin. Taloustiedettä lukevat pääsevät tutustumaan juurikin tällaisiin prosesseihin opinnoissaan.
Lisäksi Brownin liike ja tämänlainen hyppyprosessi ovat matemaattisesti kohtalaisen selkeitä ja toimivia, ainakin muihin vaihtoehtoihin verrattuna. Siksi tämä yhdistelmä on hyvin yleinen tapa rakentaa satunnaisia funktioita.
Ja tarina jatkuu...
Toki joukkoon mahtuu vielä muunkinlaisia rakennuskeinoja. Mikään laki ei esimerkiksi vaadi, että satunnaiset kertoimet olisivat toisistaan riippumattomia. Samoin asioita voidaan yleistää kahteen tai useampaan ulottuvuuteen. Kahdessa ulottuvuudessa saadaan satunnainen vuorimaisema:

Ulottuvuuden kasvaessa tosin kasvavat myös tekniset ongelmat. Alussa nähdyn valkoisen kohinan kaltaiset ongelmatapaukset muuttuvat yleisemmiksi ja vielä ilkeämmiksi. Äärettömät summat eivät enää suppenekaan ilman mystisiä kikkakolmosia, joita fyysikot ovat kehitelleet saadakseen mallinsa toimimaan.
Lienee turha sanoakaan, että hankalasti käsiteltävät jutut tunnetaan myös nimellä "kiinnostava matemaattinen tutkimuskohde" ja siksi Helsingissäkin useampi väitöskirjatutkija painii näiden olioiden kanssa.
Lopuksi pieni huomio: Todennäköisyyslaskentaa yliopistossa lukeville täytyy lisätä tähän pieni täsmennys. Useimpiin väitteisiin pitää kirjoittaa perään "melkein varmasti". Esimerkiksi Brownin liike on jatkuva vain melkein varmasti, eli on mahdollista saada epäjatkuva funktio – sen todennäköisyys vain sattuu olemaan nolla.
Myöskin kakkos- ja kolmoskohtien funktioissa on oikeasti pieni ero: kolmoskohdassa funktio ei ala ja pääty samaan arvoon. Tämä puute olisi helppo korjata valitsemalla ensimmäinen jana vakiofunktioksi, mutta muuten menetelmä pysyy samana.
Ymmärtänet, minkä takia ohitan tämänlaiset yksityiskohdat yllä. Tekniset detaljit ovat välillä turhauttavia, vaikka niistä täytyykin olla tietoinen. Alan ammattilaisille "melkein varmasti" on jatkuva taustaoletus.
Ei kommentteja:
Lähetä kommentti
Kommentit ovat moderoituja — yritän hyväksyä kommenttisi mahdollisimman pian. Voit kirjoittaa kommenttiin LaTeX-koodia tai yksinkertaista HTML-merkintää: lue lisää Kommentointi-sivulta.