Huonosti käyttäytyvät funktiot

Yläkoulussa opitaan, mitä funktio tarkoittaa. Alkuun kirjaimilla laskemisessa on reippaasti sulattelemista, mutta sen jälkeen homma alkaa helpottua. Muutaman lukiokurssin jälkeen kaavaan sijoittamiset, kuvaajan piirtämiset ja derivaatan nollakohdan etsimiset sujuvat kuin vettä vain. Tämä kuitenkin on valheellinen käsitys, joka jättää katseen ulkopuolelle ison osan maailmasta.

Useimmat funktiot nimittäin ovat kaikkea paitsi kivoja.

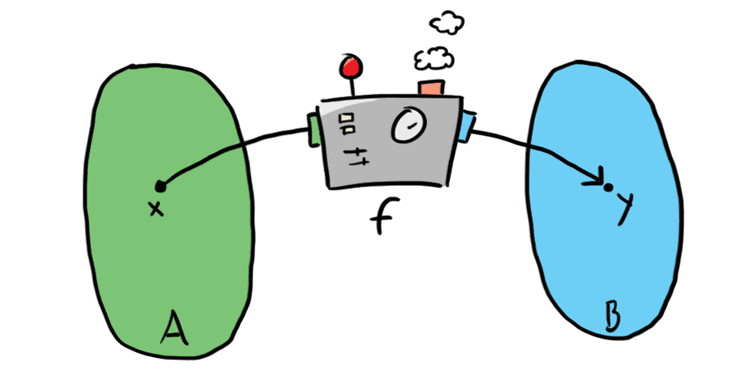
Lukion oppikirjassa sanotaan, että funktio on sääntö, joka liittää määrittelyjoukon jokaiseen alkioon $x$ jonkin maalijoukon alkion $y = f(x)$. Aiemmassa opintojen vaiheessa puhutaan usein funktiokoneesta, joka ottaa sisään luvun, tekee sille jotain ja pullauttaa tuloksen ulos.

Aika monelle funktio ja kaava ovat sama asia, eikä mikään ihme. Lukiossa käytännössä kaikki funktiot esitetään kivoina kaavoina, joissa seikkailevat $x$:n potenssit sekä muut kumppanit. Kaikkein erikoisin tapaus on paloittain määritelty funktio, jossa kaava riippuu siitä, missä päin lukusuoraa ollaan:

\[ f(x) = \begin{cases} x, \quad \text{ kun } x \leq 0,\\ \sin x, \quad \text{ kun } x > 0. \end{cases} \]

Tämännäköiset funktiot, yhdellä tai monella muuttujalla, ovat toki käytännöllisiä ja kivoja. Niitä voi aiheellisesti kutsua hyvin käyttäytyviksi — ja tämä muuten on oikea matemaattinen termi. Tutuista palikoista tutuilla operaatioilla kasatut funktiot ovat melkein aina (joitakin yksittäisiä pisteitä lukuunottamatta) jatkuvia, derivoituvia, integroituvia ja kivasti laskettavia.

Mikään laki vain ei vaadi näin olevan: voihan funktiokoneen sisällä olla vaikka mitä! Viimeistään yliopistomatikassa funktion ja kaavan liitto rikotaan. Esimerkiksi nämä ovat ihan yhtä päteviä funktioita kuin kaikki muutkin:

• Funktio, joka kääntää kokonaisluvun numerot takaperin. Esimerkiksi $f(123) = 321$.
• Funktio, joka jättää luvun desimaaliesitykseen pelkät kakkoset ja korvaa muut numerot nollilla. Esimerkiksi $f(12.2342) = 2.2002$.
• Funktio, jonka arvo on $1$ rationaaliluvuille ja $-1$ irrationaaliluvuille. Esimerkiksi $f(1/2) = 1$ ja $f(\pi) = -1$.

Nämä funktiot ovat paljon helpompia kuvailla sanoin kuin kaavoilla! Nämä myöskin ovat keskenään hyvin erilaisia tarkastella. Ensimmäinen on yllättävän helppo tutkia: ei ole vaikeaa uskoa, että $f(f(a)) = a$, oli $a$ mikä kokonaisluku tahansa, tai että palindromiluvuille funktio ei tee mitään. Toisesta on paljon vaikeampi sanoa mitään. Ja kolmas taas...

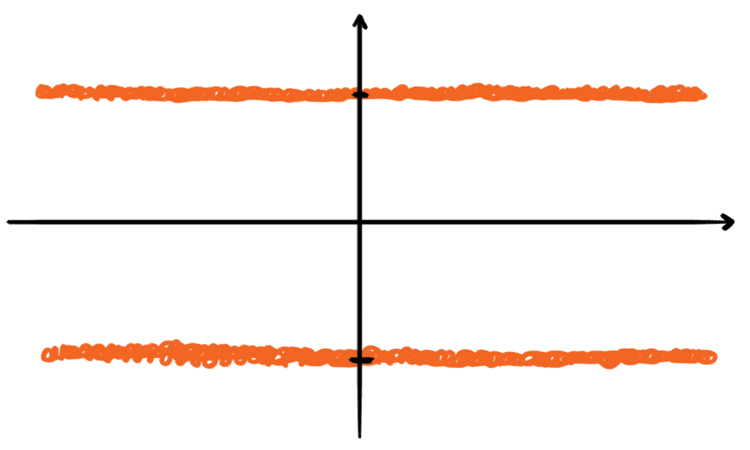
...sanotaanko, että siitä ja sen kavereista oppii pitämään yliopiston analyysin kursseilla. Se on malliesimerkki huonosti käyttäytyvästä funktiosta. Se ei ole jatkuva missään pisteessä, koska jokaisen rationaaliluvun välissä on irrationaalilukuja ja toisin päin. Koska se ei ole jatkuva, sitä ei voi myöskään derivoida tai integroida. Mutta otapa siitä itseisarvo, ja yllättäen saatkin ihanan vakiofunktion, jolle kaikki äskeiset onnistuvat! Tämä pikku funktio on loistava vastaesimerkki arkeen ja juhlaan — tai ehkä parempi kielikuva on "talossa ja puutarhassa".

Hassua kyllä, funktion ei tarvitse edes olla kovin omituisen näköinen johtaakseen syvälle suohon. Otetaanpa semmoinen kaveri kuin $\sin(x^2)$.

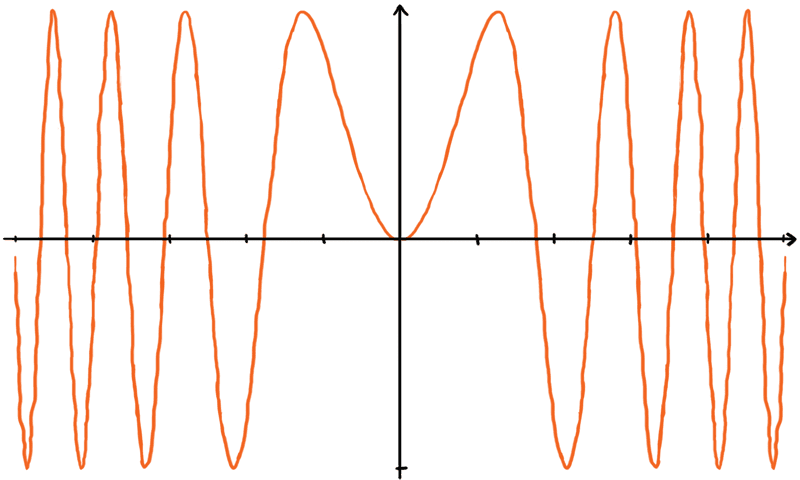
Ei näytä kovin pahalta taikka vaaralliselta ainakaan nollan lähistöllä. Voin luvata, että se on erittäin kiltisti jatkuva. Pitkää matikkaa tarpeeksi lukeneelle ei tuota mitään vaikeuksia derivoida sitä: ulkofunktion derivaatta kertaa sisäfunktion derivaatta ja tulos on $2x \cos(x^2)$. Mutta mitenkäs on sen integraalin laita? Toisin sanottuna, minkä funktion derivaatta on $\sin(x^2)$?

Jos sijoitusmenetelmä on sinulle tuttu, saatat ajatella, ettei tuo niin paha ole. Suosittelen kokeilemaan ennen kuin jatkat lukemista.

Älä pahastu, jos et osaa. Jos onnistut, olet joko tehnyt virheen tai todistanut parisataa vuotta matemaattista analyysia vääräksi. Ensimmäinen vaihtoehto on huomattavasti todennäköisempi.

Jutun juju on nimittäin se, että funktion $\sin(x^2)$ integraalifunktiota ei voi kirjoittaa tuttujen alkeisfunktioiden avulla. (Teknisesti ottaen äärettömän pitkä tapa on olemassa, mutta sellaisia ei lasketa.) Integraalifunktio tunnetaan Fresnelin integraalina, ja sille kyllä tunnetaan koko joukko ominaisuuksia ja likiarvojen laskumenetelmiä. Se ei ole yhtään huonompi kuin oppikirjoista tutut integrointikaavat, sitä vain ei voi kirjoittaa samalla tavalla kuin muita.

Tilastoihin tutustunut tietää toisenkin ikävästi integroituvan funktion. Normitetulla normaalijakaumalla on tiheysfunktio

\[ f(x) = \frac{1}{2\pi} e^{-x^2 / 2}. \]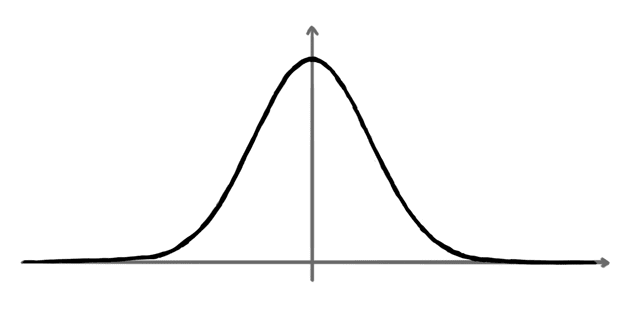

Tiheysfunktion määritelmään kuuluu, että sen integraali yli koko lukusuoran on tasan $1$. Käyttökelpoisen jakauman määritelmään kuuluu, että integraalifunktion arvot ovat järkevästi laskettavissa. Kumpikin kyllä luonnistuu normaalijakaumalta, mutta integraalin tarkka arvo on

\[ \int_{-\infty}^x f(x)~dx = \frac 1 2 \left( 1 + \mathrm{erf}\left( \frac{x}{\sqrt 2} \right) \right), \]

ja $\mathrm{erf}$ taas kerran jotain, mitä ei voi kirjoittaa äärelliselle määrälle paperia alkeisfunktioiden sekoituksena. Ja nyt puhuttiin normaalijakaumasta, joka kuvaa todella montaa mitattavaa luonnonilmiötä! Entäs sitten vielä oudommat funktiot?

On helppoa kuvitella, että edellä ehdottamieni funktioiden lisäksi on vielä paljon kummallisempia ja vaikeammin kuvattavia sääntöjä. Itse asiassa lähes kaikki reaalimuuttujan funktiot ovat tällaisia kuriositeetteja, joita ei voi kirjoittaa kaavana eikä edes pitkällisenä sääntökirjana. Ne vain ovat totaalisen satunnaisia. Tämä on väistämätön seuraus siitä, että reaalilukuja on äärettömästi.

Kaikkia mahdollisia funktioita, niin kaavoja kuin kummallisuuksiakin, voi kuitenkin käsitellä, kunhan tietää, mikä on sallittua ja mikä ei — ja siinä nämä patologiset tapaukset ovat paikallaan. Ilman hyviä vastaesimerkkejä ei ilmenisi tarvetta määritellä käsitteitä vedenpitävästi. Analyysi on nykymuodossaan juuri siksi, että aiemmat versiot eivät pystyneet selittämään erikoisia funktioita aukottomasti. Siksi yliopiston analyysin kurssikirja painaa tuhottomasti, vaikkei sisällä juuri mitään uutta lukioon nähden.

Jos emme tiedä, mikä on mahdotonta, emme oikeastaan tiedä, mikä on mahdollista. Ja siksi teoreetikot rakastavat huonosti käyttäytyviä funktioita.