Yhteenlaskun salattu elämä

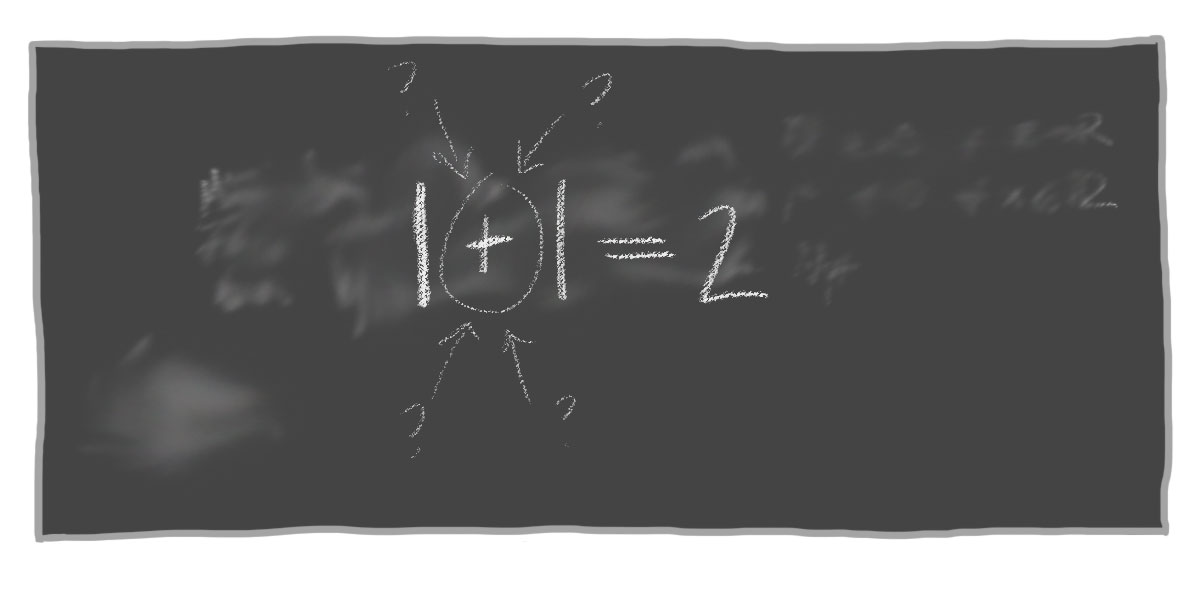
Ensimmäisenä matikasta tulee mieleen laskeminen. Matematiikan laitoksella aktiviteettina on kaikki paitsi laskeminen. Nyt kuitenkin lasketaan, mutta matemaatikon tapaan.

Matemaatikontaimi laskee $1+1=2$. Muutaman vuoden koulutuksen jälkeen otetaan askel käsitteellisempään suuntaan. Nyt paperissa lukeekin $1+x=2$ ja tehtävänä olisi selvittää $x$. Tämä hupi tunnetaan myös algebrana. Yliopistomatematiikassa askelia otetaankin sitten maratonin verran. Kun päästään abstraktiin algebraan, tutkintaan laskutoimituksessa joutuu $+$. Yhteenlasku voi tuntua maailman yksinkertaisimmalta asialta, mutta näin asian ei tietenkään tarvitse olla.

Keksitään näin alkajaisiksi uudentyyppinen yhteenlasku. Siinä missä tavanomainen 3000-luvun eaa. yhteenlasku toimii luvuilla, meidän versiomme toimii sanoilla. Sovitaan että $\oplus$ (kutsutaan tätä vaikka sananlaskuksi) liittää kaksi sanaa toisiinsa suomen kielen sääntöjen mukaisesti. Siis vaikkapa

\[ \text{makkara} \oplus \text{siili} = \text{makkarasiili}. \]

Tavallisesta plussasta erottumiseksi tällaiset spesiaalisummat on tapana piirtää ympyrän sisään, etteivät ne innostu leviämään liian kanssa. Tämä sananlaskumme vaikuttaa aika järkevältä operaatiolta, eihän tekstinpätkien pötköksi pistäminen kuulosta kovin kaukaahaetulta. Ohjelmointia harrastaville ainakin on ilmiselvää, että juuri tällä tavoin tekstin summaaminen toimii.

Kuitenkin nämä kaksi yhteenlaskua ovat kovin erilaiset. Ala-asteelta asti on ollut selvää, että $1+2$ ja $2+1$ ovat ihan samat asiat. Mutta mitäpä on

\[ \text{auto} \oplus \text{kauppa} \]

ja mitä puolestaan

\[ \text{kauppa} \oplus \text{auto}? \]

Tätä ominaisuutta, joka tavallisella yhteenlaskulla on ja sananlaskulla ei, kutsutaan vaihdannaisuudeksi. Sekä vaihdannaiset että epävaihdannaiset puuhat ovat kaikille tuttuja: yhteen- ja kertolaskuissa järjestyksellä ei ole väliä, mutta $1-2$ ei ainakaan ole $2-1$.

Kun kerta molemmat keissit ovat koulussa koeteltuja, voisi aiheellisesti tulla mieleen kysyä: "Mitä välii?" No sitä välii on, että yhtälönratkaisu menee vaikeammaksi ilman vaihdannaisuutta. Kouluhommissa sitä ei vielä huomaa, mutta vaikkapa matriiseja pyöritellessä pitää miettiä, kummalle puolelle kertolaskun kirjoittaa!

Sananlaskulla on kuitenkin yksi kiva yhteenlaskun ominaisuus: ei ole väliä, mitä laskee ensin.

\[ (\text{auto} \oplus \text{kauppa}) \oplus \text{auto} \]

ja

\[ \text{auto} \oplus (\text{kauppa} \oplus \text{auto}) \]

tuottavat tismalleen saman liiketoimen, joka olisi kokenut kumipyöräistä sekatavaraliikettäkin nopeamman sukupuuton, jos koskaan olisi rullannut teille. Vähennyslasku ei pysty tähänkään vähään, vaan

\[ (1 - 1) - 1 = -1, \quad 1 - (1 - 1) = 1. \]

Ennen kuin päästään viimeiseen ominaisuuteen, pitää määritellä uusi sana. Neutraalialkio tarkoittaa semmoista lukua, joka ei tee yhtään mitään. Yhteenlaskun neutraalialkio on pyöreä nolla, koska $0+x=x$ aina, iankaikkisesti ja myös toisinpäin summattuna. Kertolaskun neutraalialkio ei ole nolla, mutta aika lähellä — keksit varmaan mikä.

Neutraalialkio itsessään ei ole kovin kiinnostava juttu, mutta sen avulla voi määritellä jotain jännempää. Kaikkihan muistavat ainakin hämärästi sellaisen sanan kuin vastaluku. Ykkösen vastaluku on miinus yksi ja niin edelleen. Luku plus vastaluku on nolla elikkä neutraalialkio. Tämä on kiinnostava juttu, ja vastaluvusta puhutaan yleisemmin käänteisalkiona.

Jokaisella luvulla $x$ on vastaluku $-x$. Samoin kertolaskussa kaikilla luvuilla on käänteisluku $1/x$... paitsi nollalla, koska nollaa ei saa laittaa jakoviivan alle sakon ja maailmanlopun uhalla. Mutta mikä on sananlaskun käänteisalkio?

Neutraalialkio lienee lyhyt ja ytimekäs "". Ei mitään siis. Sana ei pahemmin muutu, jos siihen ei lisää mitään. Mutta keksipä sellainen sana, jonka voi kirjoittaa toisen perään niin, että jäljelle ei jää mitään. Eikä nyt kirjoiteta pyyhekumilla vaan kuulakärkikynällä!

Yhteenlaskulla on siis aina käänteisalkio, kertolaskulla yhtä poikkeusta lukuunottamatta ja sananlaskulla vain tylsimmässä mahdollisessa tapauksessa: ei mitään plus ei mitään on ei mitään, eli tyhjä sana on oma käänteissanansa. Jotta juttu olisi vielä vähän monimutkaisempi, voidaan rajautua tiettyyn osaan lukuja. Jos miinusmerkkiset luvut unohdetaan, ei vastalukujakaan ole millään muulla kuin nollalla.

Näiden ominaisuuksien perusteella erilaisia laskutoimituksia voidaan niputtaa yhteen. Yhteenlasku ja kertolasku ovat kumpikin vaihdannaisia. Plussaus ja miinustaminen eivät toimi ihan samoin, koska suluilla on väliä. Sanojen ja lukujen yhteenlaskut ovat hyvin kaukana toisistaan, mutta sananlasku ja kokonaislukujen kertolasku ovatkin erittäin samankaltaisia.

Kun laskutoimitukset luokittelee ryhmiksi, kunniksi, renkaiksi ja muiksi oudosti nimetyiksi häppäsvärkeiksi, pystyy kerralla todistamaan kaikkiin päteviä ominaisuuksia. Mutta mitäs hyötyä siitä sitten on?

No ainakin tästä jutusta saa ihan loistavaa huumoria. Joku vääräleuka oli keksinyt laitoksen käytävälle ihan uutta genreä edustavan sanaleikin:

Heh! Heh heh...

...anteeksi. Vakavammin ottaen algebran alan perusta on näissä luokitteluissa. Samaan syssyyn pystyy ymppäämään esimerkiksi kappaleiden symmetrioita — kooltaan rajattujen lukujoukkojen laskut ja kuvioiden peilaukset sekä pyörittelyt ovatkin sama asia!

Tällä puuhastelulla on kauaskantoiset seuraukset, ja siksi melkein minkä tahansa matematiikan alan eteen pystyy kirjoittamaan "algebrallinen". Muun muassa Rubikin kuution analyysi perustuu algebraan, mutta yksi ensimmäisistä isoista tuloksista liittyy yhtälöihin. Jokainen matikan yo-kokeeseen valmistautuva osaisi unissaankin ladella, että toisen asteen yhtälön $ax^2+bx+c=0$ ratkaisut löytyvät kaavasta

\[ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. \]

Samanlaiset kaavat löytyvät kolmannen ja neljännen asteen yhtälöille, mutta niitä ei löydy oppilaiden muistista tai edes muuten kaikkitietävästä MAOLista. Yksi syy ongelmaan on se, että neljännen asteen ratkaisukaava näyttää tältä — tosin tästä kuvasta ei liene hyötyä:

Lienee sanomattakin selvää, että viidennen asteen ratkaisukaava vasta hirviö onkin. Siinä vain oli se ongelma, että vuosisatojen yrittämisestä huolimatta kukaan ei löytänyt sitä. Kaikki yritykset kompastuivat johonkin yhtälöön, jota kaava ei osannutkaan ratkaista.

1800-luvun alkupuolella norjalainen Niels Henrik Abel yritti itsekin ensin keksiä ratkaisukaavaa ja pääsi aika pitkällekin tuhoontuomitussa yrityksessä, mutta sitten hän älysi tehdä U-käännöksen. Hyödyntämällä tätä uutta algebraa hän todisti, ettei viidennen asteen ratkaisukaavaa ole mahdollistakaan löytää, koska sitä ei ole olemassa. Näin hän vapautti matemaatikot jahtaamasta yhtä olematonta hirviötä ja etsimään uusia.

Ja niitähän algebrasta löytyi. Monsteriryhmä (tuttavallisemmin Ystävällinen jätti) syntyy 196 883-ulotteisen kappaleen pyörityksistä. Sen merkitys on tosin aivan oma tarinansa.